Os momentos mais dramáticos no desenvolvimento da Física são aqueles quando grandes sínteses acontecem, onde fenômenos que previamente pareciam er distintos são subitamente revelados como sendo apenas diferentes aspectos da mesma coisa. A história da Física é a história de tais sínteses, e o sucesso da ciência física baseia-se principalmente no fato de que somos capazes de sintetizar.
Talvez o momento mais dramático no desenvolvimento da Física durante o século XIX ocorreu para J. C. Maxwell um dia na década de 1860 quando combinou as leis da eletricidade e magnetismo com as leis do comportamento da luz. Como resultado, as propriedades da luz pforam parcialmente desvendadas – essa antiga e sutil coisa que de tão importante e misteriosa foi necessária uma criação especial para ela quando o Gênesis foi escrito. Maxwell poderia ter dito, quando terminou sua descoberta, “Faça-se a eletricidade e o magnetismo, e se fará a luz!”.
Para esse momento culminante foi necessária uma longa preparação apra a descoberta gradual e a revelação das leis da eletricidade e do magnetismo. Essa história é, em suma, a seguinte. Descobertas gradualmente, as propriedades da eletricidade e magnetismo, das forças elétricas de atração e repulsão e das forças magnéticas mostraram que, embora essas forças sejam um tanto complexas, elas diminuem com o quadrado da distância. Sabemos, por exemplo, que a simples lei de Coulomb para cargas estascionárias diz que o campo da força elétrica varia inversamente com o quadrado da distância. Como consequência, para distâncias suficientemente grades, a influência de um sistema de cargas sobre outro é muito pequena. Maxwell notou que as equações ou leis que tinham sido descobertas até aquele tempo eram mutuamente inconsistentes quando ele tentou juntá0las, e para tornar consistente o sistema completo, ele teve que adicionar mais um termo às suas equações. Esse novo termo trouxe uma previsão surpreendente, que uma parte dos campos elétrico e magnético decairia bem mais devagar com a distânci do que a lei do inverso do quadrado, a saber, inversamente com a primeira potência da distância! E assim ele percebeu que correntes elétricas são capazes de afetar cargas distantes do seu local, predizendo então os efeitos básicos com os quais estamos familiarizados hoje em dia – transmissão de rádio, radar e assim por diante.
Parece um milagre que alguém falando na Europa, com meras influências elétricas, possa ser escutado a milhares de milhas de distância em Los Angeles. Como isso é possível? É porque os campos não variam com o inverso do quadrado, mas apenas inversamente com a primeira potência da distância. Finalmente, então até a própria luz foi reconhecida como influências elétrica e magnética estendendo-se sobre grandes distâncias, geradas por uma oscilação incrivelmente rápida dos elétrons nos átomos. Todos esses fonômenos são resumidos na palavra radiação, ou mais especificamente, radiação eletromagnética, pois existem um ou dois outros tipos de radiação também. Quase sempre, radiação quer dizer radiação eletromagnética.
E assim é tecido o universo. Os movimentos atômicos de uma estrela longínqua ainda têm influência suficiente, mesmo nessas grandes distâncias, para mover os elétrons do nosso olho, e assim podemos entender as estrelas. Caso essa lei não existisse, estaríamos literalmente no escuro com relação ao mundo exterior! E as ondas elétricas em uma galáxia distante cinco bilhões de anos-luz – que é o objeto mais longínquo que descobrimos até o presente – pode ainda influenciar de maneira significante e detectável as correntes no “grande prato” de um rádio telescópio. E dessa maneira somos capazes de ver as estrelas e galáxias.Vamos descrever a situação da Física no final do século XIX. Tudo o que era conhecido na época sobre as leis fundamentais é resumido a seguir.
Primeiramente, existiam as leis de força: uma força era a lei da gravitação; a força em um objeto de massa 
onde 
Em seguida, as leis de eletricidade e magnetismo, como eram conhecidas no final do século XIX, são: as forças elétricas agindo em uma carga 
Para completar essa lei, temos que fornecer as fórmulas para 
Qual é a fórmula para o campo elétrico e magnético produzido por uma carga individual? Acontece que isso é muiot coplicado, e é preciso muito estudo e sofisticação para apreciá-la. Mas isso não é o que interessa. Escrevemos a lei agora apenas para impressionar o leitor com a beleza da natureza, por assim dizer, ou seja, que é possível resumir todo conhecimento fundamental em uma única página, com a notação que já é familiar. A lei para os campos de uma carga individual é completa e precisa até onde sabemos (exceto pela mecânica quântica), mas parece um tanto complicada. Não estudaremos todas as partes agora; apenas a escrevemos para causar impressão, para mostrar que pode ser escrita, e para que possamos ver de antemão aproximadamente como se parece. Na realidade, a maneira mais útil de escrever as leis corretas da eletricidade e magnetismo não é da maneira que agora as relatamos, mas envolve o que achamos de equações de campo. Porém a notação matemática para elas é diferente e nova e, portanto, escrevemos a lei em uma forma conveniente para os cálculos, mas na notação que já conhecemos.
O campo elétrico,
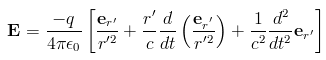
Já o campo magnético é dado por:
Escrevemos essas expressões apenas pelo propósito de mostrar a beleza da natureza, ou de um certo modo, o poder de síntese da matemática. Não pretendemos enterdor porquê é possível escrever tanto em tão pouco tempo, mas as equações acima contêm o mecanismo através do qual geradores elétricos funcionam, como a luz opera, e de todos os fenômenos de eletricidade e magnetismo. É claro que para completar a história, também precisamos conhecer alguma coisa sobre o comportament dos materiais envolvidos – as propriedades da matéria – que não são descritas apropriadamente por estas equações.
O que foi acrescentado no século XX é que as leis dinâmicas de Newton estavam todas erradas, sendo preciso introduzir a mecânica quântica para corrigí-las. As leis de Newton são válidas de uma maneira aproximada quando a escala das coisas é suficientemente grande. As leis da mecânica quântica, juntamente com as leis da eletricidade, foram apenas recentemente combinadas para formar um conjunto de leis denominados eletrodinâmica quântica. Além disso foram descobertos diversos novos fenômenos, entre eles o primeiro foi a radioatividade, descoberta por Becquerel em 1989 – que por pouco conseguiu encaixá-lo dentro do século XIX. O fenômeno da radioatividade resultou na produção do nosso conhecimento de núcleos e novos tipos de forças que não são gravitacional ou elétrica, mas novas partículas com diferentes interações, um assunto que ainda não foi totalmente esclarecido.
Para aqueles puristas que sabem mais (os professores universitários que por acaso estejam lendo isso), devemos acrescentar que quando dizemos que a equação do campo elétrico é uma expressão completa do conhecimento da eletrodinâmica, não estamos sendo completamente precisos. Existia ump roblema que não foi totalmente resolvido no final do século XIX. Quando tentamos calcular o campo devido a todas as cargas, incluindo a própria carga de prova sobre qual o campo atual, nos complicamos tentando encontrar a distância, por exemplo, da carga de si mesma, e dividir algo por essa distância, que é zero. O problema de como lidar com a parte do campo que é gerado por essa mesma carga na qual queremos que o campo atue ainda não foi resolvido até hoje. Portanto, deixemos como está; ainda não temos uma colução para o problema.
Fonte: O texto aqui reproduzido faz parte do livro Lições de Física, Volume I, capítulo 28 de Richard Feynman. Pequenas modificações foram realizadas.
segundos.
do dia solar. A taxa rotação da Terra está gradualmente diminuindo, enquanto a transição atômica do césio é muito mais constante e por isso é o hoje o padrão. Os 2 padrões diferem de apenas 1 segundo por ano.
do ponto triplo da água. Note que o sinal de grau (º) não é utilizado com kelvins.
da platina quando em seu ponto de fusão na pressão de 1 atm.
, tenha uma rentabilidade média mensal de 
e você faça depósitos mensais de 
. Quanto dinheiro você terá depois de 
meses?
e fez um depósito de 
de 
. Então por exemplo, se sua rentabilidade é de 1% ao mês, 
e 
.
![([I+D]R + D)R](https://s0.wp.com/latex.php?latex=%28%5BI%2BD%5DR+%2B+D%29R&bg=ffffff&fg=333333&s=0&c=20201002)
![{[(I+D)R + D]R + D}R](https://s0.wp.com/latex.php?latex=%7B%5B%28I%2BD%29R+%2B+D%5DR+%2B+D%7DR&bg=ffffff&fg=333333&s=0&c=20201002)
termos. No entanto, os termos dessa soma é uma progressão geométrica de grau 
tal que:
R$ 7.162.64
pois para 
a probabilidade desejada seria 1.
será o conjunto de todas as seqüências formadas com as datas dos aniversários (associamos cada data a um dos 365 dias do ano). Pode ser verificado que o conjunto das partes de um espaço amostral enumerável é uma 
-álgebra. Dessa forma, podemos tomar a 
é o quociente entre o número de elementos de 
por 
, que é o número total de seqüências de tamanho 
o evento de interesse, isto é, 
{pelo menos duas pessoas aniversariam no mesmo dia}. Para o complementar de 
{ninguém faz aniversário no mesmo dia}. Iremos calcular a probabilidade de 
com o auxílio do Princípio Fundamental da Contagem.
.
, um número relativamente baixo de pessoas, a probabilidade de pelo menos dois aniversários coincidentes já é maior que 
. A tabela a seguir apresenta alguns valores dessa probabilidade em função de 
Demônio de Maxwell 